数组算法
前缀和数组
双指针共有以下比较常用的用法:
1、前缀和数组
2、差分数组
3、寻找单链表的倒数第 k 个节点
4、寻找单链表的中点
5、判断单链表是否包含环并找出环起点
6、判断两个单链表是否相交并找出交点1.前缀和数组
解题思路: 前缀和主要适用的场景是原始数组不会被修改的情况下,频繁查询某个区间的累加和。当求区间差的时候可以直接通过第一次缓存过得值直接得出结果.
类似题目:
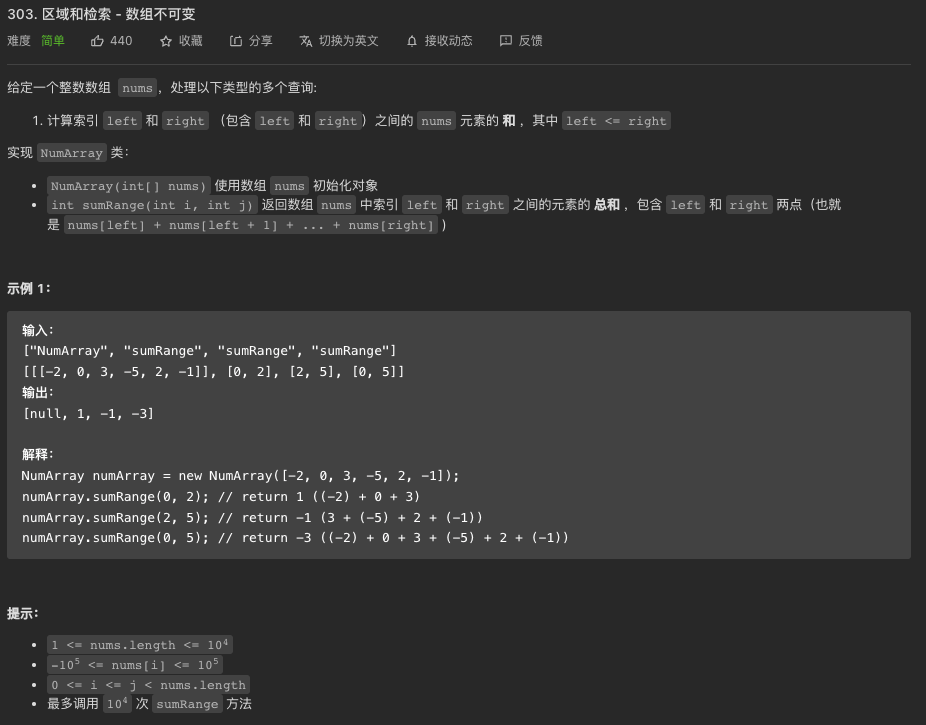
差分数组
解题思路: 差分数组的主要适用场景是频繁对原始数组的某个区间的元素进行增减, 类似于 diff 算法,
比如说,我给你输入一个数组 nums,然后又要求给区间 nums[2..6] 全部加 1,再给 nums[3..9] 全部减 3,再给 nums[0..4] 全部加 2,再给…
求 nums 数组的值是什么?
见下图
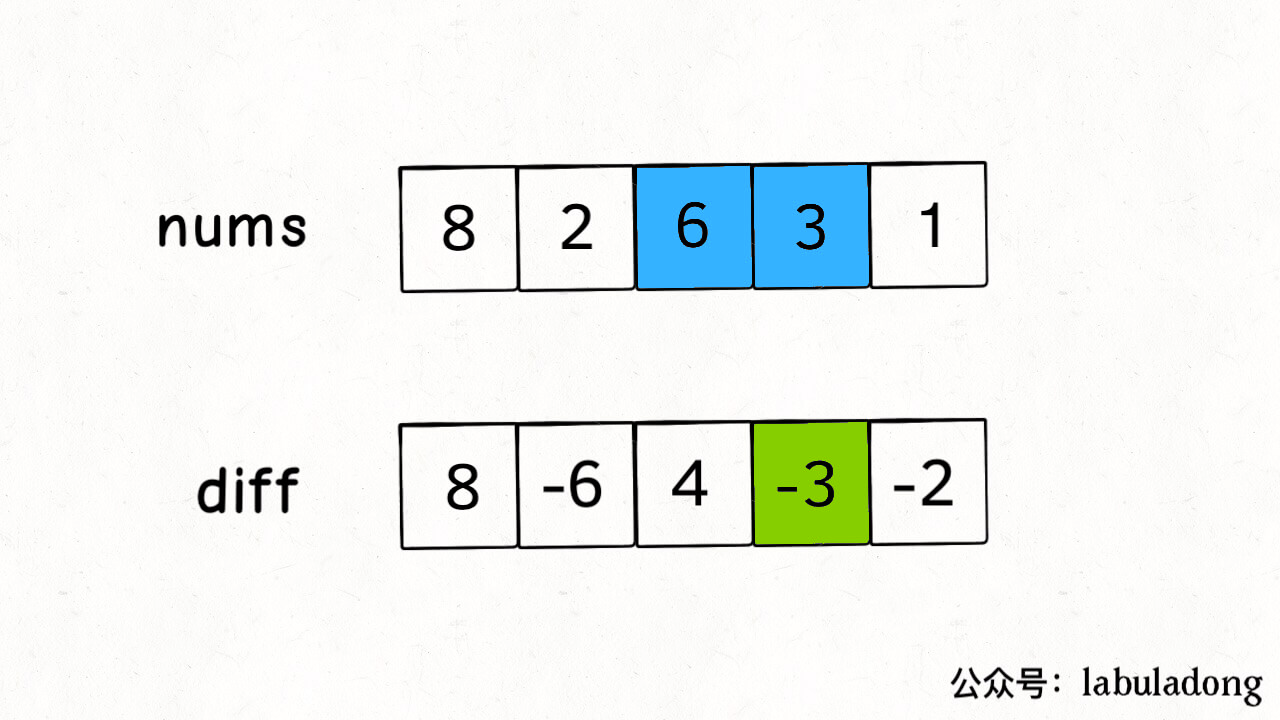
类似题目:
力扣第 370 题「 区间加法」 (opens in a new tab)
参考
二维数组
旋转矩阵 (原地旋转)
原地旋转矩阵就是在原矩阵中做定向替换,
如何「原地」旋转二维矩阵?稍想一下,感觉操作起来非常复杂,可能要设置巧妙的算法机制来「一圈一圈」旋转矩阵:

类似题目:
力扣第 48 题「 旋转图像」 (opens in a new tab)
具体见代码以及注释
class Solution {
public void rotate(int[][] matrix) {
// 遍历次数等于圈数
for (int i = 0; i < matrix.length / 2; i++) {
// 遍历次数等于 矩阵的长度 - 1, 每次便利的内容是对当前圈的最上面一行数据与其他三列做对等交换
for (int j = i; j < matrix[i].length - i - 1; j++) {
int temp;
// 交换 0 - 90 度的
temp = matrix[i][j];
matrix[i][j] = matrix[j][matrix.length - i - 1];
matrix[j][matrix.length - i - 1] = temp;
// 交换 0 度 (原 90 度) - 270 度的
temp = matrix[i][j];
matrix[i][j] = matrix[matrix.length - j - 1][i];
matrix[matrix.length - j - 1][i] = temp;
// 交换 270 度 (原 90 度) - 180 度的
temp = matrix[matrix.length - j - 1][i];
matrix[matrix.length - j - 1][i] = matrix[matrix.length - i - 1][matrix.length - j - 1];
matrix[matrix.length - i - 1][matrix.length - j - 1] = temp;
}
}
}
}
作者:jansora-2
链接:https://leetcode-cn.com/problems/rotate-image/solution/java-xuan-by-jansora-2-pu1s/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。滑动窗口
滑动窗口算法的思路是这样:
1、我们在字符串 S 中使用双指针中的左右指针技巧,初始化 left = right = 0,把索引左闭右开区间 [left, right) 称为一个「窗口」。
PS:理论上你可以设计两端都开或者两端都闭的区间,但设计为左闭右开区间是最方便处理的。因为这样初始化 left = right = 0 时区间 [0, 0)
中没有元素,但只要让 right 向右移动(扩大)一位,区间 [0, 1) 就包含一个元素 0 了。
如果你设置为两端都开的区间,那么让 right 向右移动一位后开区间 (0, 1) 仍然没有元素;
如果你设置为两端都闭的区间,那么初始区间 [0, 0] 就包含了一个元素。这两种情况都会给边界处理带来不必要的麻烦。
2、我们先不断地增加 right 指针扩大窗口 [left, right),直到窗口中的字符串符合要求(包含了 T 中的所有字符)。
3、此时,我们停止增加 right,转而不断增加 left 指针缩小窗口 [left, right),
直到窗口中的字符串不再符合要求(不包含 T 中的所有字符了)。同时,每次增加 left,我们都要更新一轮结果。
4、重复第 2 和第 3 步,直到 right 到达字符串 S 的尽头。
这个思路其实也不难,第 2 步相当于在寻找一个「可行解」,然后第 3 步在优化这个「可行解」, 最终找到最优解,也就是最短的覆盖子串。左右指针轮流前进,窗口大小增增减减,窗口不断向右滑动,这就是「滑动窗口」这个名字的来历。
类似题目:
力扣第 76 题「 最小覆盖子串」 (opens in a new tab)
class Solution {
public String minWindow(String s, String t) {
HashMap<Character, Integer> sCount = new HashMap<>();
HashMap<Character, Integer> tCount = new HashMap<>();
for (int i = 0; i < t.length(); i++) {
Character tChar = t.charAt(i);
tCount.put(tChar, tCount.getOrDefault(tChar, 0) + 1);
}
int left = 0;
int right = 0;
int match = 0;
int start = 0;
int end = Integer.MAX_VALUE;
// 遍历 s 串
while (right < s.length()) {
Character expandChar = s.charAt(right);
right++;
// 如果当前字符在 t 串中存在的, sCount 计数加 1
if (tCount.getOrDefault(expandChar, 0) > 0) {
sCount.put(expandChar, sCount.getOrDefault(expandChar, 0) + 1);
// 当前字符长度已匹配, 加一
if (sCount.getOrDefault(expandChar, 0).equals(tCount.getOrDefault(expandChar, 0))) {
match++;
}
}
while (match == tCount.size()) {
// 已存在更小的值更新,
if ((right - left) < (end - start)) {
start = left;
end = right;
}
Character narrowChar = s.charAt(left);
left++;
// 如果当前字符在 t 串中存在的, sCount 计数 - 1
if (tCount.getOrDefault(narrowChar, 0) > 0) {
// 计数减一前判断下, 剪前个数匹配, match - 1
if (sCount.getOrDefault(narrowChar, 0).equals(tCount.getOrDefault(narrowChar, 0))) {
match--;
}
sCount.put(narrowChar, sCount.getOrDefault(narrowChar, 0) - 1);
}
}
}
// 返回结果集
return (end - start) <= s.length() ? s.substring(start, end) : "";
}
}
作者:jansora-2
链接:https://leetcode-cn.com/problems/minimum-window-substring/solution/java-by-jansora-2-4lwb/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。